| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 히스토그램 평활화
- 기하 연산
- 감마 보정
- Anaconda
- 점 연산
- 컴퓨터비전
- 알고리즘
- 가상환경
- 영상알고리즘
- conda
- 파이썬
- 파이참
- tensorflow
- cv.equalizeHist
- 아나콘다
- 오픈CV
- 보간
- 영상인식
- virtual environment
- 고전 컴퓨터비전
- Pycharm
- openCV
- 동차 행렬
- 딥러닝
- Histogram Equalization
- 비전
- 오츄알고리즘
- 영역 연산
- 텐서플로
- otsu
- Today
- Total
Bongsu
영상 처리의 기본 연산(점 연산, 영역 연산, 기하 연산) 본문
이번 포스팅에서는 영상 처리의 기본 연산 3가지인 점 연산, 영역 연산, 기하 연산을 다루고자 한. 각 연산의 정의부터 알아보자.
1. 점 연산 : 점 연산은 이미지의 크기, 기하학 구조 및 로컬 구조를 변경하지 않고 픽셀 값을 수정하는 것이다. 새 픽셀 값은 이전 값에만 의존하며 이전과 동일한 위치에 사상된다.
2. 영역 연산 : 이웃 화소를 같이 고려하여 새로운 값을 결정한다. 영역 연산은 주로 컨볼루션을 통해 이루어지며, 잡음 제거 및 대비 향상을 위한 작업에서 쓰일 수 있다.
(개인적으로 찾아봤을 때, Area operation ... 이라고 검색하니 정확하게 서치 되지 않았다... 최대한 같은 내용으로 키워드를 잡자니 Convolution / Kernel function in OpenCV 로 잡았는데 Area operation과 관련한 정확한 내용 있으면 댓글을 부탁 드리고자 한다.)
3. 기하 연산 : 이미지에 적용되는 기하학적 연산은 일반적으로 이미지를 변환하고 재구성 또는 비교를 위한 연산이다. 이때 점 연산과는 다르게 이전 위치와는 다른 픽셀 값을 가져오는 데, 이러한 부분은 영상을 회전하거나 특정 부분을 확대하는 작업에서 쓰일 수 있다.
그런데 이렇게 활자로 보자니 이해가 한번에 되지 않았다. 나 같은 경우는 그림의 도움을 많이 받아 아래 남기고자 한다.
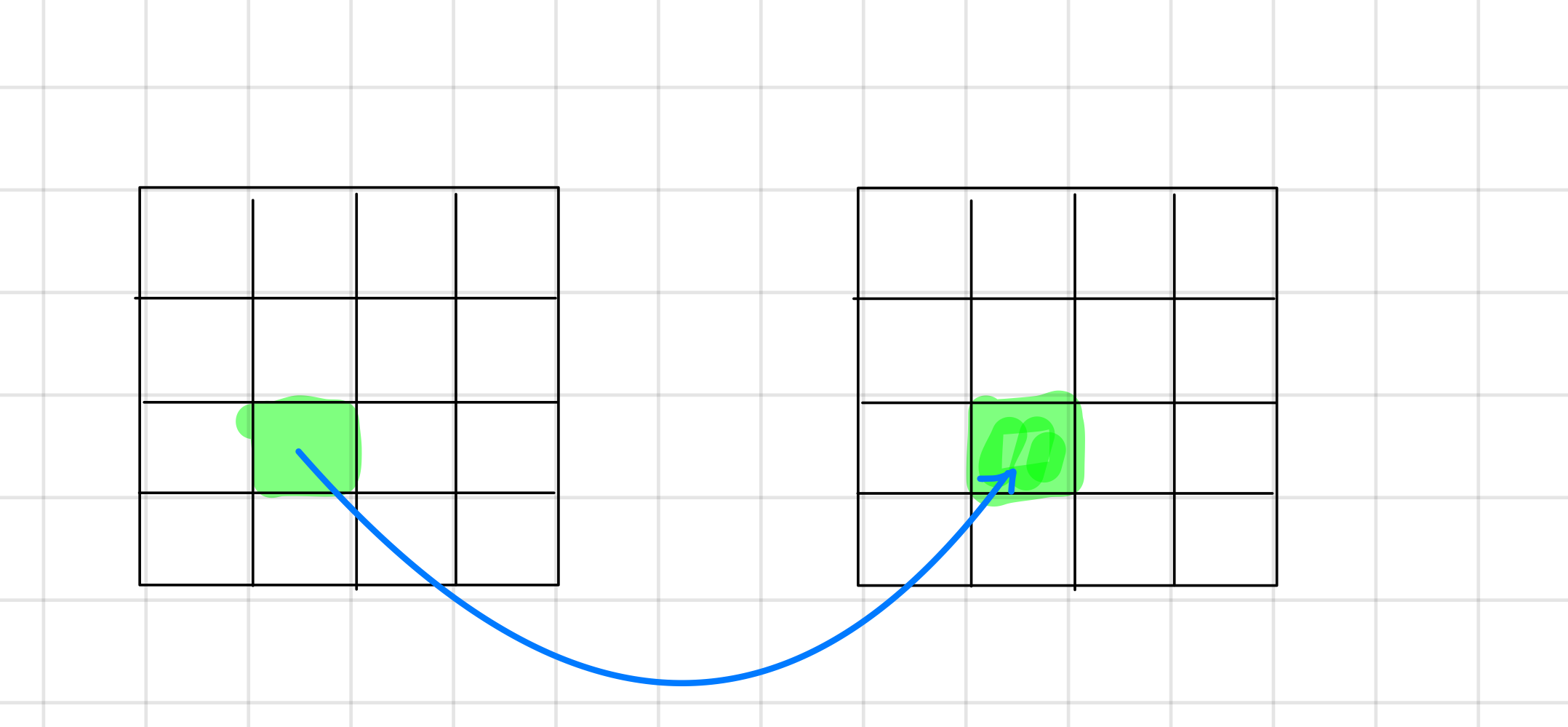


그림을 보고 설명을 보니 이해가 수월한 듯하다!
각각의 연산의 경우 대표 선수들이 존재하는데, 이 페이지에서 자세하게 적으면 글이 너무 길어질 것 같아 후에 또 포스팅 하는 것으로 하고 오늘은 그 대표주자들을 간략하게만 소개하는 것으로 하자.
1. 점 연산
점 연산의 경우, 우리 눈의 밝기 수용이 선형(Linear)적으로 반응을 하는 것이 아니라 비선형(Non-linear)으로 반응한다는 것으로 알려져 이를 이용하여 영상의 밝기를 보정하는 '감마 보정' 이 존재한다. 감마 보정은 수식이 비교적 이해가 간단하니 잠시 살펴보자.
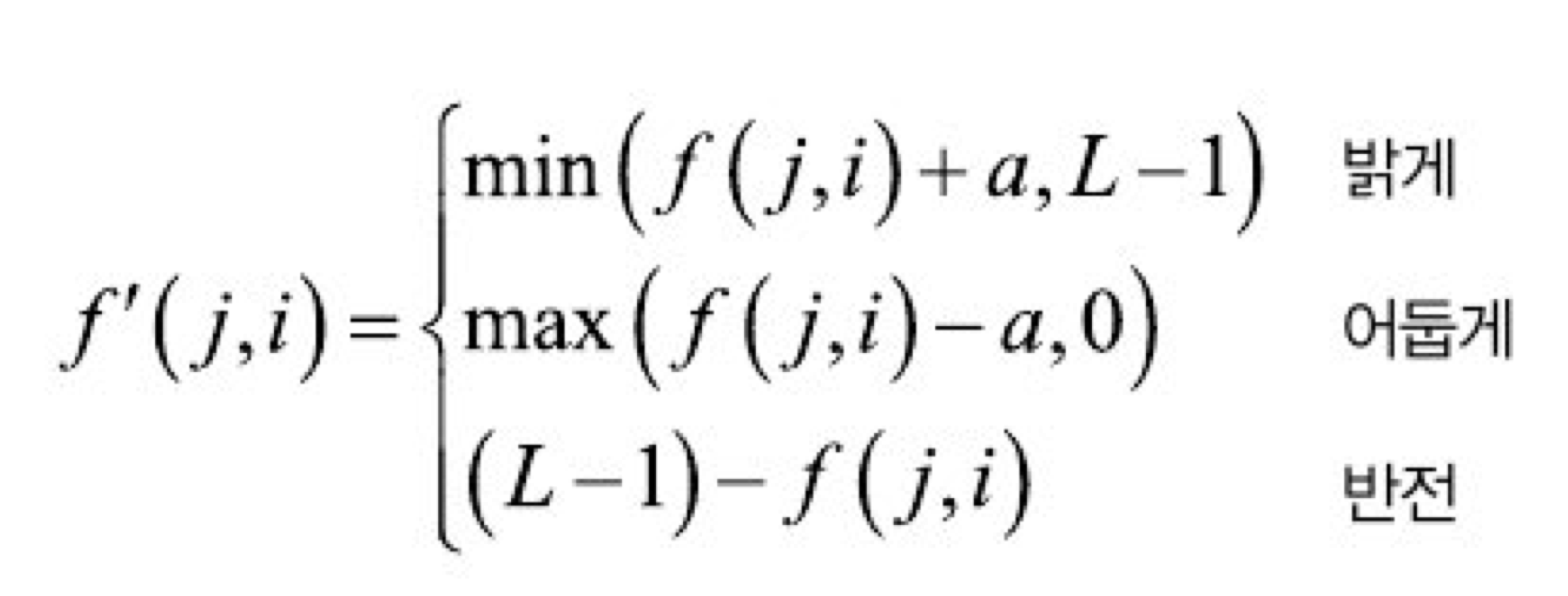

위의 식을 보면 밝게 식의 0부터 L-1 까지의 화소값 중, 최대 크기의 화소값과 해당 화소 값을 일정 값 더한 값 중 최솟값을 이용하여 아래 비선형 감마보정 식을 이용하여 밝기를 조정한다. min 값을 이용하는 이유는 최대밝기(화소값 = L-1)를 억제하기 위해서이다.
유사한 방법으로 어둡게 식도 max 값을 이용해 최소밝기(화소값 = 0)를 억제해주며 정의해 준 모습을 볼 수 있다. 반전식의 경우는 말 그대로 밝기의 반전인데, 최대 화소값에서 이전 화소값을 빼주어 밝기를 반전시켜준다.
점 연산의 대표적인 주자로는 히스토그램 평활화(Histogram equlization)가 있는데, 이는 앞서 말했듯, 후에 자세하게 포스팅하는 것으로 하자!
2. 영역 연산
사실 영역 연산은 컨볼루션(Convolution)이라는 개념이 대부분이다. 컨볼루션의 경우는 많은 이들이 아는 CNN (Convolutional Neural Network)의 그 Convolution이다.
컨볼루션을 다룰 때 쓰이는 도구가 바로 커널(Kernel) 또는 필터(Filter) 이다. 간단히 풀어쓰자면, 입력 영상의 각 화소에 필터를 적용해 곱의 합을 구하는 연산이라고 보면 된다.
이해에는 정말 시각 자료만 한 것이 없다. 여러 블로그 중 아래 그림이 매우 직관적이어서 자료를 들고왔다.

이미지 매트릭스의 각 화소에 동일한 위치의 커널 매트릭스 요소를 곱한 합을 더해보면 105 * 0 + 102* 01 + 100* 0 + 103 * -1 + 99*5 +103 * -1 + 101*0 + 98 * -1 + 104 * 0 = 89 임을 알 수 있다.
사실 이러한 필터는 여러 종류가 있으며, 각기 하는 역할마다 이름도 다르다. 대표 주자로는 스무딩 필터, 샤프닝 필터, 엠보싱 필터 등 이 존재하는 데, 스무딩 필터 중 가우시안 필터를 후에 자세하게 포스팅 하고자 한다.

좌측 스무딩 필터인 Low pass filtering 의 경우, 어떤 점의 값이 주위에 비해 아주 낮게 된다면, 해당 값과 주변을 평균하는 필터링을 통해 자신은 커지고 주위는 작아진다. 즉 이러한 필터링은 잡음을 누그러뜨리는 효과를 발휘한다. 그러나 부작용으로 경계를 흐릿하게 만드는 블러링(Blurring)이라는 부작용이 있다.
Low pass filtering 외에도 High pass filtering, Median filtering 과 같은 디테일들이 있는 데, 아래 링크에 설명이 되어 있으니 참고하면 될 것 같다.
https://www.geeksforgeeks.org/spatial-filters-averaging-filter-and-median-filter-in-image-processing/
중간의 샤프닝 필터는 스무딩 필터와 반대로 에지를 선명하게 해서 물체의 식별을 돕는 작업을 한다. 즉, 영상 에지(밝기가 급격이 변하는 부분) 근방에서 픽셀 값의 명암비가 커지도록 해야 한다는 것이다.
이렇게 샤프닝 필터를 적용하게 되면 초점이 잘 맞은 사진처럼 사물의 윤곽이 뚜렷하고 선명한 느낌이 난다. 그러나 앞서 스무딩 필터와 반대라고 말한 것과 같이 잡음을 확대한다는 부작용이 존재한다.
해당 그림의 필터는 라플라시안 연산자로 에지를 검출하며 에지 검출에 대한 더 자세한 내용은 아래 링크에 설명이 되어 있으니 참고하면 될 것 같다.
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=bsw2428&logNo=221448393580
우측의 엠보싱 필터는 물체에 돋음 느낌을 주는 필터로, 이미지의 솟음 또는 패임 효과를 준다. 이때 엠보싱 필터는 오른쪽 아래 화소에서 왼쪽 위 화소를 빼는 연산을 수행하는데, 화소값이 급격하게 변하는 부분에서는 화소가 일정 구간 밖에 존재할 수 있기에 이를 일정값 더해주고 축소해주는 변환을 하기도 한다.
간단하게 예시를 들어 0 ~ 255 범위의 화소값을 이용한다면 일반적으로 엠보싱 필터를 적용 후 각 화소값에 128을 더하여 준다.(통계적으로 -255에서 -128 구간과 128에서 255 구간을 이용하는 것이 합리적이라고 판단) 이후 Numpy 의 np.clip() 등을 이용하여 0~255 범위로 축소해준다.
자세한 코드는 구글링하면 여러 블로그에 OpenCV를 이용한 엠보싱 필터 적용 사례가 나와있으니 참조하면 될 듯 하다.
3. 기하 연산
점 연산과 영역 연산이 자기 자신 또는 이웃을 보고 값을 정하는 연산이었다면, 기하 연산은 행렬을 활용한 여러 가지 기하 변환을 통해 이전 위치와는 다른 화소값을 가져올 수 있다.
이때 쓰이는 행렬이 동차 행렬인데, 이러한 동차 행렬에 앞서 동차 좌표의 간단한 개념이 필요하다. 아래를 보자

이러한 벡터 p는 2차원 벡터 (y,x)에 1을 추가하여 3차원 벡터로 나타내었다. 이때, 동차 좌표에서는 3개의 요소에 같은 값을 곱하면 같은 좌표를 나타낸다는 것이 동차 좌표의 개념이다.
간단히 예를 들어 이해해보자면, (3, -2, 1) , (6, -4, 2), (-3, 2, -1), (9, -6, 3)은 모두 같은 좌표를 나타내며 (3, -2) 를 의미한다.
기하 변환은 이러한 동차 좌표에서 3 x 3 동차 행렬을 표현하여 여러가지 변환인 이동, 회전, 크기, 기울임을 의미한다.

이때, 동차 좌표 p에 대해 동차 행렬 T와 R을 적용 할 때, 행렬의 결합 법칙을 이용한다면 순서에 상관없이 그 표기를 표현 할 수 있다.
동차 좌표에 대해 이동 후 회전을 하는 R(Tp) 는 동차 좌표에 대해 회전을 하고 이동을 하는 T(Rp) 경우나 그 결과 값은 같다고 표현할 수 있다는 것이다.
이러한 계산의 핵심은 변환해야 하는 점이 많고 여러 단계의 변환을 적용하는 경우, 변환 행렬을 결합하여 미리 만들어 두고 점 마다 하나의 계산을 통해 행렬 곱을 하는 계산에 매우 큰 이점이 있다는 것이다.
즉 위의 예에서는 (RT) 라는 복합 행렬 변환 식을 작성해두고 이를 p 좌표에 행렬 곱을 적용하여 한 번에 계산을 할 수 있다는 것이다.
그러나 기하 연산을 통한 화소값의 경우, 화소 위치를 정수로 지정하기 때문에 영상의 일그러짐 현상이 일어나기도 한다. 이러한 이유로는 전방 변환을 통해 영상을 변환하게 된다면, 영상 곳곳에 구멍이 뚫려 노이즈와 같이 영상의 퀄리티가 낮아지는 현상이 발생하는데, 이를 에일리어싱(Aliasing)이라고 한다.
일반적인 처리법으로 안티-에일리어싱(Anti-Aliasing)이 존재한다. 대표적인 안티에일리어싱으로 후방 변환이 있는데, 전방 변환과 후방 변환의 차이는 아래 그림으로만 이해하고 자세한 내용은 해당 출처의 블로그를 참조하면 더 좋은 학습이 될 것이라 생각한다.
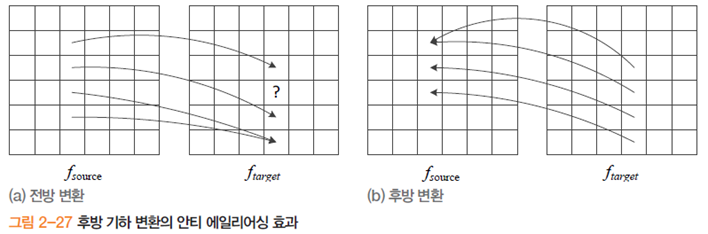
그러나 여전히 실수 좌표를 정수화 하는 문제가 남는다. 이때 이를 해결할 수 있는 방법이 보간이다.
일반적으로 OpenCV 프로그램에서 제공하는 보간으로는 최근접 이웃(INTER_NEAREST), 양선형 보간(INTER_LINEAR), 양3차 보간(INTER_CUBIC)이 존재하며 최근접 이웃의 경우 에일리어싱이 여전히 심하며, 양선형 보간과 양3차 보간을 통한 방법이 영상의 개선 정도가 높다.
정확히는 양3차 보간의 방법이 양선형 보간보다 개선 정도가 높은 데, 양선형보간은 2차원 좌표상 화소가 걸친 비율을 가중치로 이용하여 선형 보간을 이용하는 반면 양3차 보간의 경우 3차 함수를 통해 16개의 데이터 및 5회의 보간 시행을 이용하여 영상 보간을 한다. (양3차 보간이라고 하는 이유는 가중치 함수가 3차 함수 꼴을 나타내기 때문으로 구체적인 가중치 함수는 생략하겠다.) 그러나 계산량이 양3차 보간법이 양선형 보간법에 비해 훨씬 많다는 단점이 존재한다.
'컴퓨터비전' 카테고리의 다른 글
| 히스토그램 평활화 (Histogram Equalization) (0) | 2023.07.10 |
|---|---|
| 오츄 알고리즘 (Otsu Algorithm) (0) | 2023.07.03 |


